The new rsample::sliding_*() functions bring the windowing approaches used in slider to the sampling procedures used in the tidymodels framework1. These functions make evaluation of models with time-dependent variables easier2.
For some problems you may want to take a traditional regression or classification based approach3 while still accounting for the date/time-sensitive components of your data. In this post I will use the tidymodels suite of packages to:
- build lag based and non-lag based features
- set-up appropriate time series cross-validation windows
- evaluate performance of linear regression and random forest models on a regression problem
For my example I will use data from Wake County food inspections. I will try to predict the SCORE for upcoming restaurant food inspections.
Load data
You can use Wake County’s open API (does not require a login/account) and the httr and jsonlite packages to load in the data. You can also download the data directly from the Wake County website4.
library(tidyverse)
library(lubridate)
library(httr)
library(jsonlite)
library(tidymodels)Get food inspections data:
r_insp <- GET("https://opendata.arcgis.com/datasets/ebe3ae7f76954fad81411612d7c4fb17_1.geojson")
inspections <- content(r_insp, "text") %>%
fromJSON() %>%
.$features %>%
.$properties %>%
as_tibble()
inspections_clean <- inspections %>%
mutate(date = ymd_hms(DATE_) %>% as.Date()) %>%
select(-c(DATE_, DESCRIPTION, OBJECTID))Get food locations data:
r_rest <- GET("https://opendata.arcgis.com/datasets/124c2187da8c41c59bde04fa67eb2872_0.geojson") #json
restauraunts <- content(r_rest, "text") %>%
fromJSON() %>%
.$features %>%
.$properties %>%
as_tibble() %>%
select(-OBJECTID)
restauraunts <- restauraunts %>%
mutate(RESTAURANTOPENDATE = ymd_hms(RESTAURANTOPENDATE) %>% as.Date()) %>%
select(-PERMITID)Further prep:
- Join the
inspectionsandrestaurantsdatasets5 - Filter out extreme outliers in
SCORE(likely data entry errors) - Filter to only locations of
TYPErestaurant6 - Filter out potential duplicate entries7
- It’s important to consider which fields should be excluded for ethical reasons. For our problem, we will say that any restaurant name or location information must be excluded8.
inspections_restaurants <- inspections_clean %>%
left_join(restauraunts, by = c("HSISID")) %>%
filter(SCORE > 50, FACILITYTYPE == "Restaurant") %>%
distinct(HSISID, date, .keep_all = TRUE) %>%
select(-c(FACILITYTYPE, PERMITID)) %>%
select(-c(NAME, contains("ADDRESS"), CITY, STATE, POSTALCODE, PHONENUMBER, X, Y, GEOCODESTATUS))inspections_restaurants %>%
glimpse()## Rows: 30,273
## Columns: 6
## $ HSISID <chr> "04092017542", "04092017542", "04092017542", "04092~
## $ SCORE <dbl> 94.5, 92.0, 95.0, 93.5, 93.0, 93.5, 92.5, 94.0, 94.~
## $ TYPE <chr> "Inspection", "Inspection", "Inspection", "Inspecti~
## $ INSPECTOR <chr> "Anne-Kathrin Bartoli", "Laura McNeill", "Laura McN~
## $ date <date> 2017-04-07, 2017-11-08, 2018-03-23, 2018-09-07, 20~
## $ RESTAURANTOPENDATE <date> 2017-03-01, 2017-03-01, 2017-03-01, 2017-03-01, 20~Feature Engineering & Data Splits
Discussion on issue #168 suggests that some features (those depending on prior observations) should be created before the data is split9. The first and last sub-sections:
provide examples of the types of features that should be created before and after splitting your data respectively. Lag based features can, in some ways, be thought of as ‘raw inputs’ as they should be created prior to building a recipe10.
Lag Based Features (Before Split, use dplyr or similar)
Lag based features should generally be computed prior to splitting your data into “training” / “testing” (or “analysis” / “assessment”11) sets. This is because calculation of these features may depend on observations in prior splits12. Let’s build a few features where this is the case:
- Prior
SCOREforHSISID - Average of prior 3 years of
SCOREforHSISISD - Overall recent (year) prior average
SCORE(acrossHSISISD) - Days since
RESTAURANTOPENDATE - Days since last inspection
date
data_time_feats <- inspections_restaurants %>%
arrange(date) %>%
mutate(SCORE_yr_overall = slider::slide_index_dbl(SCORE,
.i = date,
.f = mean,
na.rm = TRUE,
.before = lubridate::days(365),
.after = -lubridate::days(1))
) %>%
group_by(HSISID) %>%
mutate(SCORE_lag = lag(SCORE),
SCORE_recent = slider::slide_index_dbl(SCORE,
date,
mean,
na.rm = TRUE,
.before = lubridate::days(365*3),
.after = -lubridate::days(1),
.complete = FALSE),
days_since_open = (date - RESTAURANTOPENDATE) / ddays(1),
days_since_last = (date - lag(date)) / ddays(1)) %>%
ungroup() %>%
arrange(date)The use of .after = -lubridate::days(1) prevents data leakage by ensuring that this feature does not include information from the current day in its calculation13 14.
Data Splits
Additional Filtering:
We will presume that the model is only intended for restaurants that have previous inspections on record15 and will use only the most recent seven years of data.
data_time_feats <- data_time_feats %>%
filter(date >= (max(date) - years(7)), !is.na(SCORE_lag)) %>%
# keep just records at date of initial publishing
filter(date <= ymd(20201012))Initial Split:
After creating our lag based features, we can split our data into training and testing splits.
initial_split <- rsample::initial_time_split(data_time_feats, prop = .8)
train <- rsample::training(initial_split)
test <- rsample::testing(initial_split)Resampling (Time Series Cross-Validation):
For this problem we should evaluate our models using time series cross-validation16. This entails creating multiple ordered subsets of the training data where each set has a different assignment of observations into “analysis” or “assessment” data17.
Ideally the resampling scheme used for model evaluation mirrors how the model will be built and evaluated in production. For example, if the production model will be updated once every three months it makes sense that the “assessment” sets be this length. We can use rsample::sliding_period() to set things up.
For each set, we will use three years of “analysis” data for training a model and then three months of “assessment” data for evaluation.
resamples <- rsample::sliding_period(train,
index = date,
period = "month",
lookback = 36,
assess_stop = 3,
step = 3)I will load in some helper functions I created for reviewing the dates of our resampling windows18.
devtools::source_gist("https://gist.github.com/brshallo/7d180bde932628a151a4d935ffa586a5")
resamples %>%
extract_dates_rset() %>%
print() %>%
plot_dates_rset() ## # A tibble: 7 x 6
## splits id analysis_min analysis_max assessment_min assessment_max
## <list> <chr> <date> <date> <date> <date>
## 1 <split [7789/92~ Slic~ 2015-02-10 2018-02-28 2018-03-01 2018-05-31
## 2 <split [8196/88~ Slic~ 2015-05-01 2018-05-31 2018-06-01 2018-08-31
## 3 <split [8547/90~ Slic~ 2015-08-03 2018-08-31 2018-09-04 2018-11-30
## 4 <split [8848/10~ Slic~ 2015-11-02 2018-11-30 2018-12-03 2019-02-28
## 5 <split [9370/98~ Slic~ 2016-02-01 2019-02-28 2019-03-01 2019-05-31
## 6 <split [9704/99~ Slic~ 2016-05-02 2019-05-31 2019-06-03 2019-08-30
## 7 <split [10216/9~ Slic~ 2016-08-01 2019-08-30 2019-09-03 2019-11-27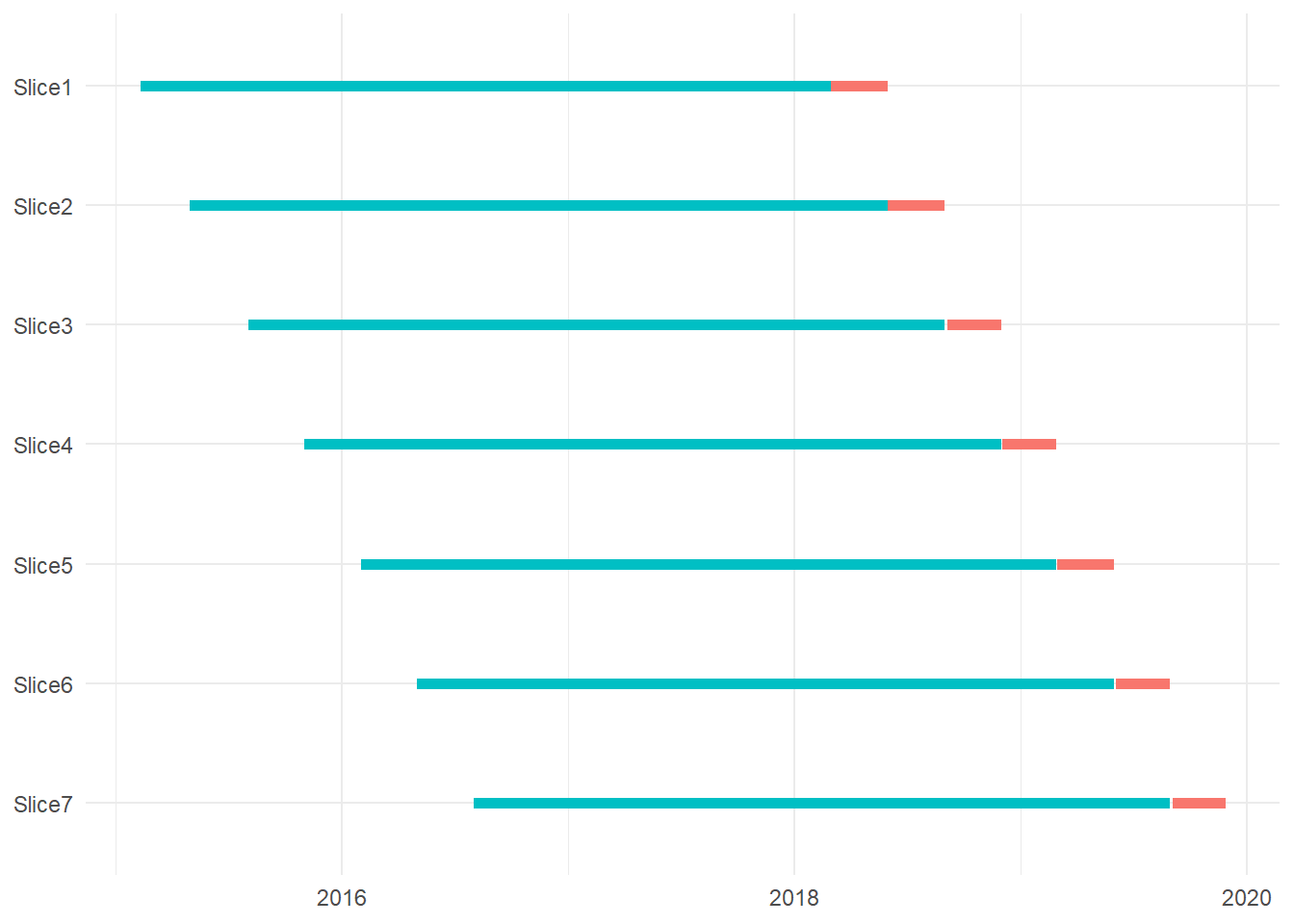
For purposes of overall Model Evaluation, performance across each period will be weighted equally (regardless of number of observations in a period)19 20.
Other Features (After Split, use recipes)
Where possible, features should be created using the recipes package21. recipes makes pre-processing convenient and helps prevent data leakage.
It is OK to modify or transform a previously created lag based feature in a recipes step. Assuming that you created the lag based input as well as your resampling windows in an appropriate manner, you should be safe from data leakage issues when modifying the variables during later feature engineering steps22.
Some features / transformations I’ll make with recipes:
- collapse rare values for
INSPECTORandTYPE - log transform
days_since_openanddays_since_last - add calendar based features
rec_general <- recipes::recipe(SCORE ~ ., data = train) %>%
step_rm(RESTAURANTOPENDATE) %>%
update_role(HSISID, new_role = "ID") %>%
step_other(INSPECTOR, TYPE, threshold = 50) %>%
step_string2factor(one_of("TYPE", "INSPECTOR")) %>%
step_novel(one_of("TYPE", "INSPECTOR")) %>%
# note that log transformations are completely superfluous for the random
# forest model fit (is only valuable for the linear mod)
step_log(days_since_open, days_since_last) %>%
step_date(date, features = c("dow", "month")) %>%
update_role(date, new_role = "ID") %>%
step_zv(all_predictors()) Let’s peak at the features we will be passing into the model building step:
prep(rec_general, data = train) %>%
juice() %>%
glimpse() ## Rows: 14,594
## Columns: 12
## $ HSISID <fct> 04092013767, 04092014115, 04092014155, 04092015493, 0~
## $ TYPE <fct> Inspection, Inspection, Inspection, Inspection, Inspe~
## $ INSPECTOR <fct> Johanna Hill, Jennifer Edwards, Angela Myers, Angela ~
## $ date <date> 2015-02-10, 2015-02-10, 2015-02-10, 2015-02-10, 2015~
## $ SCORE_yr_overall <dbl> 95.59897, 95.59897, 95.59897, 95.59897, 95.59845, 95.~
## $ SCORE_lag <dbl> 98.0, 98.5, 94.5, 96.5, 90.5, 97.5, 93.0, 93.5, 91.0,~
## $ SCORE_recent <dbl> 98.40000, 98.87500, 97.37500, 92.50000, 94.25000, 95.~
## $ days_since_open <dbl> 8.383662, 8.248529, 8.235626, 7.568896, 6.723832, 8.0~
## $ days_since_last <dbl> 4.890349, 5.407172, 5.187386, 5.081404, 5.749393, 4.6~
## $ SCORE <dbl> 98.0, 98.5, 98.0, 87.0, 94.5, 95.5, 95.5, 90.0, 94.0,~
## $ date_dow <fct> Tue, Tue, Tue, Tue, Wed, Wed, Wed, Wed, Wed, Wed, Wed~
## $ date_month <fct> Feb, Feb, Feb, Feb, Feb, Feb, Feb, Feb, Feb, Feb, Feb~Model Specification and Training
Simple linear regression model:
lm_mod <- parsnip::linear_reg() %>%
set_engine("lm") %>%
set_mode("regression")
lm_workflow_rs <- workflows::workflow() %>%
add_model(lm_mod) %>%
add_recipe(rec_general) %>%
fit_resamples(resamples,
control = control_resamples(save_pred = TRUE))ranger Random Forest model (using defaults):
rand_mod <- parsnip::rand_forest() %>%
set_engine("ranger") %>%
set_mode("regression")
set.seed(1234)
rf_workflow_rs <- workflow() %>%
add_model(rand_mod) %>%
add_recipe(rec_general) %>%
fit_resamples(resamples,
control = control_resamples(save_pred = TRUE))parsnip::null_model:
The NULL model will be helpful as a baseline Root Mean Square Error (RMSE) comparison.
null_mod <- parsnip::null_model(mode = "regression") %>%
set_engine("parsnip")
null_workflow_rs <- workflow() %>%
add_model(null_mod) %>%
add_formula(SCORE ~ NULL) %>%
fit_resamples(resamples,
control = control_resamples(save_pred = TRUE))See code in Model Building with Hyperparameter Tuning for more sophisticated examples that include hyperparameter tuning for glmnet23 and ranger models.
Model Evaluation
The next several code chunks extract the average performance across “assessment” sets24 or extract the performance across each of the individual “assessment” sets.
mod_types <- list("lm", "rf", "null")
avg_perf <- map(list(lm_workflow_rs, rf_workflow_rs, null_workflow_rs),
collect_metrics) %>%
map2(mod_types, ~mutate(.x, source = .y)) %>%
bind_rows() extract_splits_metrics <- function(rs_obj, name){
rs_obj %>%
select(id, .metrics) %>%
unnest(.metrics) %>%
mutate(source = name)
}
splits_perf <-
map2(
list(lm_workflow_rs, rf_workflow_rs, null_workflow_rs),
mod_types,
extract_splits_metrics
) %>%
bind_rows()The overall performance as well as the performance across splits suggests that both models were better than the baseline (the mean within the analysis set)25 and that the linear model outperformed the random forest model.
splits_perf %>%
mutate(id = forcats::fct_rev(id)) %>%
ggplot(aes(x = .estimate, y = id, colour = source))+
geom_vline(aes(xintercept = mean, colour = fct_relevel(source, c("lm", "rf", "null"))),
alpha = 0.4,
data = avg_perf)+
geom_point()+
facet_wrap(~.metric, scales = "free_x")+
xlim(c(0, NA))+
theme_bw()+
labs(caption = "Vertical lines are average performance as captured by `tune::collect_metrics()`")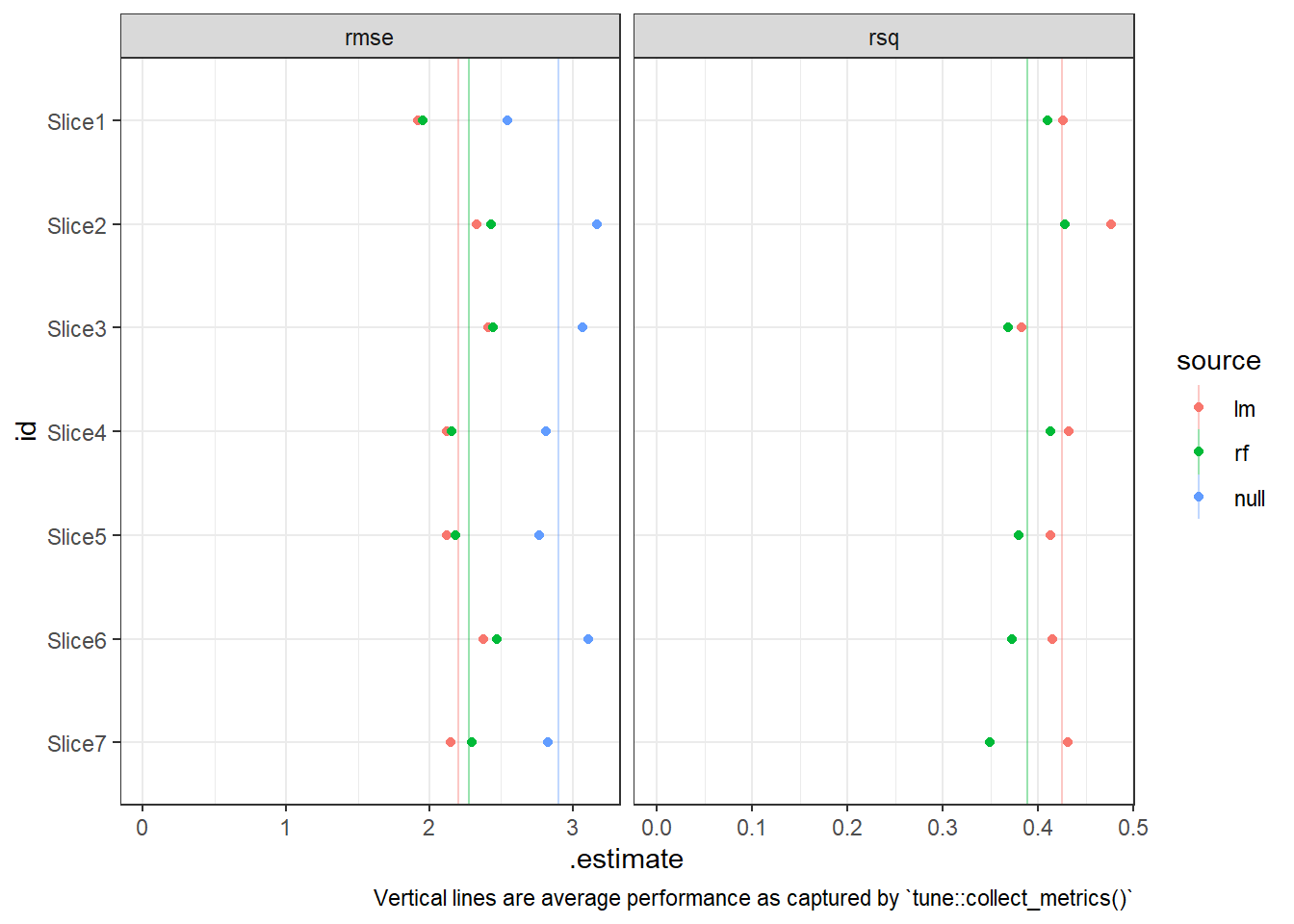
We could use a paired sample t-test to formally compare the random forest and linear models’ out-of-sample RMSE performance.
t.test(
filter(splits_perf, source == "lm", .metric == "rmse") %>% pull(.estimate),
filter(splits_perf, source == "rf", .metric == "rmse") %>% pull(.estimate),
paired = TRUE
) %>%
broom::tidy() %>%
mutate(across(where(is.numeric), round, 4)) %>%
knitr::kable() | estimate | statistic | p.value | parameter | conf.low | conf.high | method | alternative |
|---|---|---|---|---|---|---|---|
| -0.0707 | -4.3075 | 0.0051 | 6 | -0.1109 | -0.0305 | Paired t-test | two.sided |
This suggests the better performance by the linear model is statistically significant.
Other potential steps:
There is lots more we could do from here26. However the purpose of this post was to provide a short tidymodels example that incorporates window functions from rsample and slider on a regression problem. For more resources on modeling and the tidymodels framework, see tidymodels.org or Tidy Modeling with R27.
Appendix
Model Building with Hyperparameter Tuning
Below is code for tuning a glmnet linear regression model (use tune to optimize the L1/L2 penalty)28.
rec_glmnet <- rec_general %>%
step_dummy(all_predictors(), -all_numeric()) %>%
step_normalize(all_predictors(), -all_nominal()) %>%
step_zv(all_predictors())
glmnet_mod <- parsnip::linear_reg(penalty = tune(), mixture = tune()) %>%
set_engine("glmnet") %>%
set_mode("regression")
glmnet_workflow <- workflow::workflow() %>%
add_model(glmnet_mod) %>%
add_recipe(rec_glmnet)
glmnet_grid <- tidyr::crossing(penalty = 10^seq(-6, -1, length.out = 20), mixture = c(0.05,
0.2, 0.4, 0.6, 0.8, 1))
glmnet_tune <- tune::tune_grid(glmnet_workflow,
resamples = resamples,
control = control_grid(save_pred = TRUE),
grid = glmnet_grid)And code to tune a ranger Random Forest model, tuning the mtry and min_n parameters29.
rand_mod <- parsnip::rand_forest(mtry = tune(), min_n = tune(), trees = 1000) %>%
set_engine("ranger") %>%
set_mode("regression")
rf_workflow <- workflow() %>%
add_model(rand_mod) %>%
add_recipe(rec_general)
cores <- parallel::detectCores()
set.seed(1234)
rf_tune <- tune_grid(rf_workflow,
resamples = resamples,
control = control_grid(save_pred = TRUE),
grid = 25)Resources
- Link on doing regressions in slider: https://twitter.com/dvaughan32/status/1247270052782637056?s=20
- Rstudio lightning talk on
slider: https://rstudio.com/resources/rstudioconf-2020/sliding-windows-and-calendars-davis-vaughan/ modeltimepackage that appliestidymodelssuite to time series and forecasting problems: https://business-science.github.io/modeltime/ (business-science course has more fully developed training materials on this topic as well)
These were announced with version 0.0.8. The help pages for
rsample(as well as thesliderpackage) are helpful resources for understanding the three types of sliding you can use, briefly these are:sliding_window(): only takes into account order / position of datessliding_index(): slide according to an indexsliding_period(): slide according to an index and set k split points based on period (and other function arguments)
rsample::sliding_index()andrsample::sliding_period()are maybe the most useful additions as they allow you to do resampling based on a date/time index. Forsliding_index(), you usually want to make use of thestepargument (otherwise it defaults to having a split for every observation).I found
rsample::sliding_period()easier to get acquantied with thanrsample::sliding_index(). However within thesliderpackage I foundslider::sliding_index()easier to use thanslider::sliding_period(). Perhaps this makes sense as when setting sampling windows you are usually trying to return an object with far fewer rows, that is, collapsed to k number of rows (unless you are doing Leave-One-Out cross-validation). On the other hand, thesliderpackage is often used in amutate()step where you often want to output the same number of observations as are inputted. Perhaps then it is unsurprising the different scenarios when theindexvsperiodapproach feels more intuitive.↩︎Previously users would have needed to use
rsample::rolling_origin().↩︎As opposed to a more specialized time-series modeling approach.↩︎
This dataset is updated on an ongoing basis as Food Inspections are conducted. This makes it a poor choice as an example dataset (because results will vary if running in the future when more data has been collected). I used it because I am familiar with the dataset, it made for a good example, and because I wanted a publicly documented example of pulling in data using an API (even a simple one).↩︎
There is also “violations” dataset available, which may have additional useful features, but which I will ignore for this example.↩︎
For this example I’m pretending that we only care about predicting
SCOREfor restaurants… as opposed to food trucks or other entities that may receive inspections.↩︎Or at least cases where historical data is claiming there were multiple inspections on the same day.↩︎
In some cases you may need to be more careful than this and exclude information that are proxies for inappropriate fields as well. For example, pretend that the
INSPECTORs are assigned based on region. In this case,INSPECTORwould be a proxy for geographic information and perhaps warranting exclusion as well (in certain cases).↩︎Into training / testing sets or analysis / assessment sets.↩︎
An “Analysis” / “Assessment” split is similar to a “training” / “testing” split but within the training dataset (and typically multiple of these are created on the same training dataset). See section 3.4 of Feature Engineering and Selection… for further explanation.]↩︎
It is important that these features be created in a way that does not cause data leakage.↩︎
Which would not be available at the time of prediction.↩︎
I’m a fan of the ability to use negative values in the
.afterargument:
↩︎This is a fairly obscure feature in {slider}, but I love it. Don’t want the current day in your rolling window? Set a negative
— Davis Vaughan (@dvaughan32) February 27, 2020.aftervalue to shift the end of the window backwards. For example:
On day 5
.before = days(3)
.after = -days(1)
Includes days:
[2, 4] https://t.co/rG0IGuTj1cIf I did not make this assumption, I would need to impute the time based features at this point.↩︎
Two helpful resources for understanding time series cross-validation:
↩︎An “Analysis” / “Assessment” split is similar to a “training” / “testing” split but within the training dataset (and typically multiple of these are created on the same training dataset). See section 3.4 of Feature Engineering and Selection… for further explanation.]↩︎
I’ve tweeted previously about helper functions for reviewing your resampling scheme:
↩︎❤️new
— Bryan Shalloway (@brshallo) October 10, 2020rsample::sliding_*()funs by @dvaughan32. It can take a minute to check that all arguments are set correctly. Here are helper funs I've used to check that my resampling windows are constructed as intended: https://t.co/HhSjuRzAsB may make into an #rstats #shiny dashboard. pic.twitter.com/sNloHfkh4aNote that using
rsample::sliding_period()is likely to produce different numbers of observations between splits.↩︎It could also make sense to weight performance metrics by number of observations. One way to do this, would be to use a control function to extract the predictions, and then evaluate the performance across the predictions. In my examples below I do keep the predictions, but end-up not doing anything with them. Alternatively you could weight the performance metric by number of observations. The justification for weighting periods of different number of observations equally is that noise may vary consistently across time windows – weighting by observations may allow an individual time period too much influence (simply because it happened to be that there were a greater proportion of inspections at that period).↩︎
For each split, this will then build the features for the assessment set based on each analysis set.↩︎
Although I just do a simple
step_log()transform below, more sophisticated steps on lag based inputs would also be kosher, e.g.step_pca(). However there is a good argument that many of these should be done prior to arecipesstep. For example, say you have missing values for some of the lag based inputs – in that case it may make sense to use a lag based method for imputation, which may work better than say a mean imputation using the training set. So, like many things, just be thoughtful and constantly ask youself what will be the ideal method while being careful that, to the question of “will this data be available prior to the prediction?” that you can answer in the affirmitive.↩︎Our number of observations is relatively high compared to the number of features, so there is a good chance we will have relatively low penalties. While working interactively, I did not see any substantive difference in performance.↩︎
Remember that this is not weighted by observations, so each assessment set impacts the overall performance equally, regardless of small differences in number of observations.↩︎
There is no baseline performance for Rsquared because the metric itself is based off amount of variance that is explained compared to the baseline (i.e. the mean).↩︎
You would likely iterate on the model building process (e.g. perform exploratory data analysis, review outliers in initial models, etc.) and eventually get to a final set of models to evaluate on the test set.↩︎
I added a few other links to the Resources section in the Appendix↩︎
Our number of observations is relatively high compared to the number of features, so there is a good chance we will have relatively low penalties.↩︎
This was taking a long time and is part of why I decided to move the tuned examples to the Appendix.↩︎